Flat leaves obscure the sky when one looks up towards the zenith. Towards the horizon, however, they let light come through. The contrary applies to erect leaves. The inclination angle of the leaves therefore affect the appearance of the canopy on the hemispherical photograph. Because not all leaves have the same angle, their statistical distribution has to be taken into account when estimating the LAI.
If leaves are facing all directions with the same probability, then one could imagine to move them (without any rotation) to the surface of a sphere and this sphere would then be covered all around with the same density of leaves. The statistical leaf angle distribution is thus called spherical. If there are more erect and less flat leaves, then the sphere should be replaced by an ellipsoid with a vertical axis longer then its horizontal axes. On the contrary if there are more flat than erect leaves. This model (ELAD = ellipsoidal leaf angle distribution) is quite convenient for calculations and in most cases not far from reality.
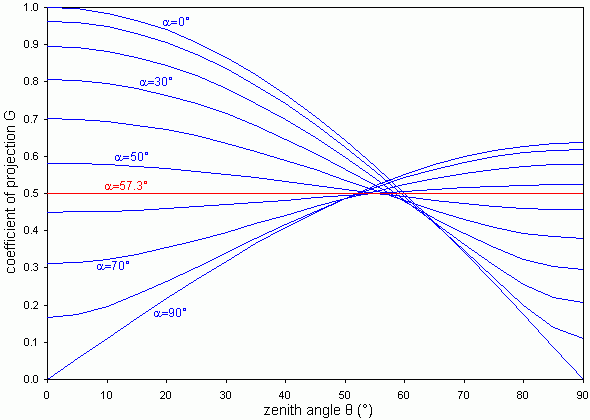
In the ellipsoidal model, there is just one parameter which can vary: the ratio between the horizontal radii and the vertical radium of the ellipsoid. This ratio is noted x and called ELADP, meaning ellipsoidal leaf angle distribution parameter. Knowing the ELADP, it is possible to calculate an average leaf angle α (alpha). For example α = 1 rad = 57° for x = 1 (spherical distribution).
The ratio between the apparent area of a leaf and its real area is the projection coefficient G. It is a function of both the leaf inclination α (alpha) and the direction from which the leaf is looked at, conveniently given as the angle θ (theta) to the zenith. For ellipsoidal leaf area distributions, G behaves according to the following curves. Note: G is constant for a sphere (α = 57°) and shows the largest changes with either very flat or very erect ellipsoids, but it is always close to 0.5 for a zenith angle near 57°.